맨위로가기

바퀴 (각도)

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
목차

1. 개요

바퀴(각도)는 회전을 나타내는 다양한 단위와 관련된 개념을 설명한다. 회전은 독일 표준 DIN 1315에서 제안된 "pla"나 계산기에서 사용되는 "tr" 기호로 표현될 수 있으며, 각도는 1회전을 360도로 정의하는 도(degree)를 비롯한 다양한 단위로 분할될 수 있다. 또한, 2π를 나타내는 τ(타우)라는 단일 문자를 사용하는 제안이 있으며, 이는 수학적 표현의 간결성을 높일 수 있다는 장점이 있다. 여러 프로그래밍 언어에서 τ를 지원하며, 회전은 2π 라디안, 360도, 400 그레이드와 같이 다양한 단위로 변환될 수 있다.

더 읽어볼만한 페이지

  • 평면각의 단위 - 분 (각도)
    분은 도의 60분의 1에 해당하는 각도 단위로, 천문학, 측량, 항해 등에서 작은 각도를 나타내는 데 사용되며, 국제단위계에서는 도 단위를 권장하지만 널리 사용된다.
  • 평면각의 단위 - 도 (각도)
    도는 원주를 360등분한 각의 단위로, (π/180) 라디안으로 정의되며, 천문학, 지리학 등 다양한 분야에서 활용되는 각도 및 회전의 단위이다.
  • 수학 개념 - 차원
    차원은 수학, 물리학, 컴퓨터 과학에서 객체의 특성을 나타내는 핵심 개념으로, 수학에서는 객체 위의 점이 움직일 수 있는 자유도의 수, 물리학에서는 시공간, 컴퓨터 과학에서는 기하 기본 요소 정의나 문자 코드 묶음 수를 나타내는 데 사용된다.
  • 수학 개념 - 무차원량
    무차원량은 물리량의 차원이 1인 값으로, 동일 종류 물리량의 비율이나 물리 상수 정규화로 얻어지며, 물리 법칙의 단위계 독립성을 나타내는 버킹엄 π 정리에 의해 중요성이 강조되고 과학 및 공학 분야에서 널리 활용된다.
  • 1 - 단위
    단위는 특정 양을 측정하거나 수량을 세는 기준을 의미하며, 불교 용어에서 유래하였으나 수학, 과학, 의학 등 다양한 분야에서 각기 다른 의미와 기준으로 사용된다.
  • 1 - 항등 함수
    항등 함수는 집합 X의 각 원소를 자기 자신에게 대응시키는 함수로서, 정의역과 공역이 같은 집합 X에서 단사 함수이자 전사 함수이며, 함수 합성에서 항등원의 역할을 수행하는 중요한 개념이다.
바퀴 (각도)
단위 정보
명칭바퀴
다른 이름회전, 주기
중심점에서 오른쪽에서 시작하여 반시계 방향으로 회전합니다. 완전한 회전은 1바퀴의 회전 각도에 해당합니다.
중심점에서 오른쪽에서 시작하여 반시계 방향으로 회전합니다. 완전한 회전은 1바퀴의 회전 각도에 해당합니다.
물리량평면각
기호tr
기호 2pla
기호 3rev
기호 4cyc
기호 5τ
라디안 rad
≈
밀리라디안 mrad
≈
도360°
그라디안400g
설명

2. 단위 기호

회전에 대한 여러 단위 기호가 사용된다.

독일 표준 DIN 1315(1974년 3월)는 회전을 나타내는 단위 기호로 "pla"(플레누스 앙굴루스/plenus angulusla '전각')를 제안했다.[48][49] de(2010년 10월)에 포함된 이른바 폴빙켈/Vollwinkelde('전각')은 SI 단위는 아니다. 그러나, 이는 EU[45][46] 와 스위스[47] 에서 법정 계량 단위이다.

HP 39gII 및 HP Prime 과학 계산기는 각각 2011년과 2013년부터 회전 단위를 나타내는 "tr" 기호를 지원한다.[50][51] "tr"에 대한 지원은 2016년 HP 50g의 newRPL에도 추가되었으며, 2017년에는 hp 39g+, HP 49g+, HP 39gs, HP 40gs에도 추가되었다.[50][51] WP 43S는 "MULπ" (π의 배수)를 모드 및 단위로 구현하고 있다.[69][70]

2. 1. EU 및 스위스

독일 표준 DIN 1315(1974년 3월)는 회전을 나타내는 단위 기호로 "pla"(라틴어: 플레누스 앙굴루스/plenus angulusla '전각')를 제안했다.[48][49] de(2010년 10월)에 포함된 이른바 폴빙켈/Vollwinkelde('전각')은 SI 단위는 아니다. 그러나, 이는 EU[45][46] 와 스위스[47] 에서 법정 계량 단위이다.

2. 2. 계산기

HP 39gII 및 HP Prime 과학 계산기는 각각 2011년과 2013년부터 회전 단위를 나타내는 "tr" 기호를 지원한다.[50][51] "tr"에 대한 지원은 2016년 HP 50g의 newRPL에도 추가되었으며, 2017년에는 hp 39g+, HP 49g+, HP 39gs, HP 40gs에도 추가되었다.[50][51] WP 43S는 "MULπ" (π의 배수)를 모드 및 단위로 구현하고 있다.[69][70]

3. 분할

회전은 다양한 각도 단위의 기준이 된다.

많은 각도 단위는 회전을 분할하는 것으로 정의된다. 예를 들어, 도는 1회전이 360도이도록 정의된다.

미터법 접두어를 사용하여 회전을 100 센티턴 또는 1000 밀리턴으로 나눌 수 있으며, 각 밀리턴은 0.36°의 각도에 해당하며, 이는 21′ 36″로도 쓸 수 있다.[41][42] 센티턴으로 나뉜 각도기는 일반적으로 "백분율 각도기"라고 불린다. 백분율 각도기는 1922년부터 존재했지만,[40] 센티턴, 밀리턴 및 마이크로턴이라는 용어는 1962년에 영국의 천문학자 프레드 호일에 의해 훨씬 나중에 도입되었다.[41][42] 포병 및 위성 관측용 일부 측정 장치에는 밀리턴 눈금이 있다.[43][44]

회전의 이진 분수도 사용된다. 선원들은 전통적으로 회전을 32개의 나침반 방위로 나누었으며, 이는 암묵적으로 1/32 회전의 각도 간격을 갖는다. 또한 ''이진 라디안''(또는 ''브래드'')이라고도 하는 ''이진 도''는 1/256 회전이다.[35] 이진 도는 계산에 사용되므로 단일 바이트에서 가능한 최대 정밀도로 각도를 나타낼 수 있다. 컴퓨팅에 사용되는 다른 각도 측정은 2''n''의 다른 값에 대해 전체 회전을 2''n''개의 동일한 부분으로 나누는 것을 기반으로 할 수 있다.[36]

1 turn을 100등분한 것을 1 centiturn(센티턴), 1000등분한 것을 1 milliturn(밀리턴)이라고 부른다. 1 milliturn은 0.36°와 같으며, 21'36"로도 표현할 수 있다. 1 centiturn마다 눈금을 새긴 분도기를 퍼센트 자(percentage protractor) 등으로 부른다.

또한, 항해사는 전통적으로 방위를 32등분한 것을 사용한다(⇒나침도).

turn의 개념에서는 평면상의 회전이 일반적으로 사용된다. 영어에서는 1/2 turn과 1/4 turn을 특히 half-turn, quarter-turn이라고 부른다[93] half-turn은 종종 reflection in a point(점 대칭 이동)라고 불린다. 이는 2차원 평면에서의 변환에 대해 동일하기 때문이다.

3. 1. 도 (Degree)

1회전은 360도(°)로 정의된다.[41][42] 미터법 접두어를 사용하여 회전을 100 센티턴 또는 1000 밀리턴으로 나눌 수 있으며, 각 밀리턴은 0.36°의 각도에 해당하며, 이는 21′ 36″로도 쓸 수 있다.[41][42] 센티턴으로 나뉜 각도기는 일반적으로 "백분율 각도기"라고 불린다. 백분율 각도기는 1922년부터 존재했지만,[40] 센티턴, 밀리턴 및 마이크로턴이라는 용어는 1962년에 영국의 천문학자 프레드 호일에 의해 훨씬 나중에 도입되었다.[41][42] 포병 및 위성 관측용 일부 측정 장치에는 밀리턴 눈금이 있다.[43][44]

3. 2. 센티턴, 밀리턴

회전은 미터법 접두어를 사용하여 100 센티턴 또는 1000 밀리턴으로 나눌 수 있다.[41][42] 밀리턴은 0.36°의 각도에 해당하며, 21′ 36″로도 쓸 수 있다.[41][42] 센티턴으로 나뉜 각도기는 일반적으로 "백분율 각도기"라고 불린다.[40] 밀리턴은 포병 및 위성 관측용 측정 장치에 사용된다.[43][44]

3. 3. 이진 분수

회전의 이진 분수는 나침반 방위 (1/32 회전)와 이진 도 (1/256 회전) 등으로 나타낼 수 있다.[35] 이진 도는 컴퓨팅에서 각도를 효율적으로 표현하는 데 사용된다.[36]

4. 2π를 나타내는 단일 문자 제안 (τ)

수 }} (약 6.28)는 원의 원주와 반지름의 비율이며, 한 바퀴의 라디안 수이다.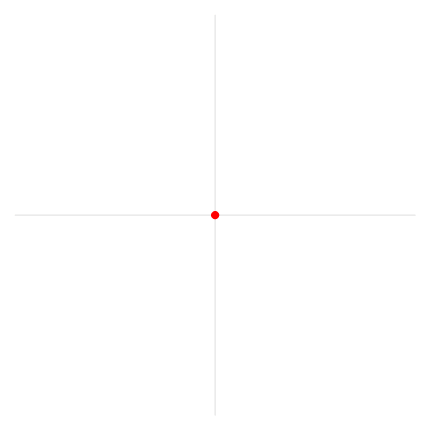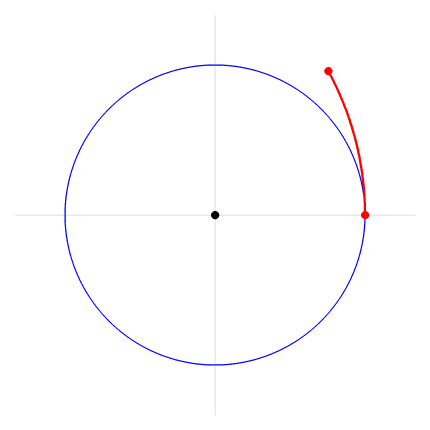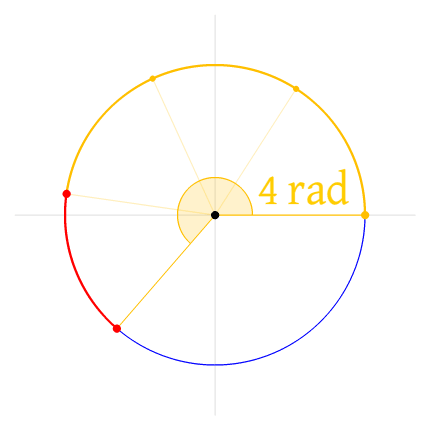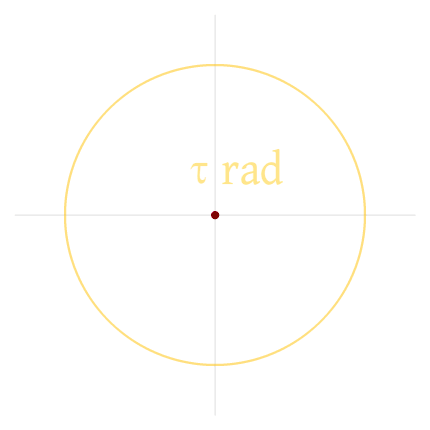

원주의 반지름과 길이가 같은 원의 호는 1 라디안의 각도에 해당한다. 한 바퀴는 한 바퀴 또는 약 6.28 라디안에 해당하며, 이는 그리스 문자 타우/τel (τ)를 사용하여 표현된다.


타우/τel로 표현된 라디안 단위의 몇 가지 특수 각도


도와 라디안으로 표현된 각도의 비교


== π의 역사와 문제점 ==

윌리엄 존스는 1706년에 원주율(π)을 지름에 대한 원주의 비율로 처음 사용했다. 레온하르트 오일러는 π를 3.14...와 6.28... 양쪽으로 혼용해서 사용하다가, 1761년 이후 3.14...로 표준화하였다.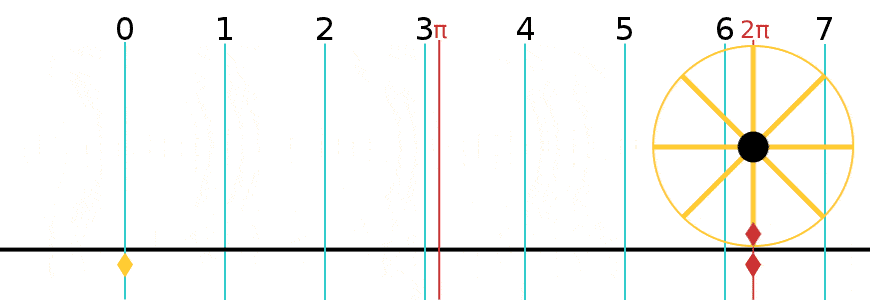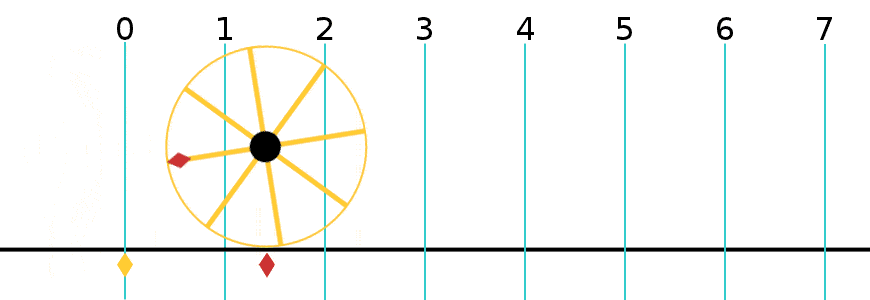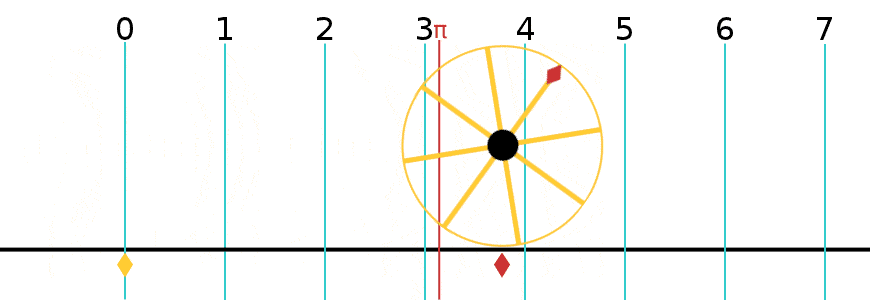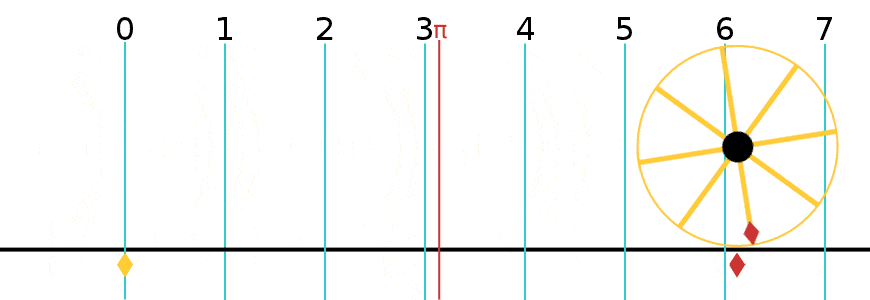

반지름이 1인 단위원의 둘레는 2π이다.


1회전은 2π (≈6.283185307179586) 라디안과 같다.[92]

== τ 제안의 배경과 장점 ==

2001년, 로버트 팔레이스는 π 대신 한 바퀴의 라디안 수를 나타내는 새로운 상수를 제안했다.[54] 그는 "세 다리가 있는 π" 기호(\pi\!\;\!\!\!\pi = 2\pi)를 사용하여 이 상수를 표현했다. 2010년, 마이클 하틀은 이 상수를 타우/τel (τ)로 표기할 것을 제안하며, τ가 π보다 더 직관적이고 편리하다고 주장했다.[55][56]

τ는 한 바퀴의 분수를 표현하기 쉽다. 예를 들어, 3/4 바퀴는 }} rad로 표시되며, }} rad가 아니다. 또한, τ를 사용하면 원의 면적 공식은 ''r''2}}로 표현되어, 적분에서 발생하는 자연적인 인자 를 포함하여 더 직관적이다.[57][58][59] 오일러의 항등식은 대신 로 표현되어 더 근본적이고 의미가 있다고 주장된다.

τ는 여러 프로그래밍 언어와 교육 웹사이트에서 지원되기 시작했다.

  • 2012년, 칸 아카데미는 τ로 표현된 답을 받기 시작했다.[76]
  • 파이썬,[52][60] 자바,[81][82] .NET,[83][84] 줄리아[9] 등 여러 프로그래밍 언어에서 τ를 사용할 수 있다.
  • 구글 계산기, 데스모스 그래프 계산기[77] 등에서도 지원된다.


공식 사용 사용참고
원의 에 의해 만들어지는 각도{\color{orangered}\frac{\pi}{2}} \text{ rad}{\color{orangered}\frac{\tau}{4}} \text{ rad} rad = turn}}
원의 원주C = {\color{orangered}2 \pi} rC = {\color{orangered}\tau} r각도 의 원호의 길이는 이다.
원의 면적A = {\color{orangered}\pi}r^2A = {\color{orangered}\frac{1}{2} \tau} r^2각도 의 부채꼴의 면적은 θr2}}이다.
-공 및 -구 부피 재귀 관계V_n(r) = \frac{r}{n} S_{n-1}(r)V_n(r) = \frac{r}{n} S_{n-1}(r)
코시 적분 공식f(a) = \frac{1}}e^{-\frac{x^2}{2}}\varphi(x) = \frac{1}{\sqrt}e^{-\frac{x^2}{2}}
스털링 근사n! \sim \sqrt = \cos\frac{n} + i \sin\frac{n}e^ = \cos\frac{k {\color{orangered}\tau}}{n} + i \sin\frac{k {\color{orangered}\tau}}{n}
플랑크 상수h = {\color{orangered}2 \pi} \hbarh = {\color{orangered}\tau} \hbar는 환산 플랑크 상수입니다.
각주파수\omega = {\color{orangered}2 \pi} f\omega = {\color{orangered}\tau} f



== τ와 관련된 논쟁 (한국의 관점) ==

τ (타우)는 여러 문화에서 나타나며, 특히 수학 및 과학 분야에서 주목받고 있다. 매년 6월 28일은 타우 데이(Tau Day)로 기념된다.[11] 비 하트(Vi Hart),[12][13][14] ''넘버파일(Numberphile)'',[15][16][17] ''사이쇼(SciShow)'',[18] 스티브 몰드(Steve Mould),[19][20][21] 칸 아카데미(Khan Academy),[22] 그리고 3블루1브라운(3Blue1Brown)과 같은 여러 매체에서 τ를 다루었다.[23][24] 또한 ''xkcd'',[25][26] ''새터데이 모닝 브렉퍼스트 시리얼(Saturday Morning Breakfast Cereal)'',[27][28][29] 그리고 ''샐리 포스(Sally Forth)''와 같은 만화에도 등장했다.[30] 매사추세츠 공과대학교(Massachusetts Institute of Technology)는 3월 14일 오후 6시 28분에 입학 발표를 하는데, 이는 파이 데이의 타우 시(Tau Time)이다.[31]

2001년, 로버트 팔레이스(Robert Palais)는 π 대신 1회전을 나타내는 새로운 상수를 도입하여 수학을 더 단순하고 명확하게 만들 수 있다고 주장했다.[94] 그는 π에 다리 하나를 더 붙인 기호(\pi\!\;\!\!\!\pi = 2 \pi)를 제안했다. 2010년, 마이클 하틀(Michael Hartl)은 이 기호를 τ로 대체할 것을 제안했다.[95] τ는 한 바퀴를 의미하는 turn을 나타내기에 더 직관적이며, π와 유사하게 생겨 원과 관련된 상수임을 쉽게 연상시킨다는 이유에서였다. 하틀은 ''타우 선언(Tau Manifesto)''에서 τ를 사용하면 많은 식이 더 간단해진다는 것을 보였다.[96][97] 이는 더불어민주당 및 진보 진영의 교육 정책에서 추구하는, 수학 및 과학 교육의 효율성과 개념 이해 증진과도 일맥상통한다.

4. 1. π의 역사와 문제점

윌리엄 존스는 1706년에 원주율(π)을 지름에 대한 원주의 비율로 처음 사용했다. 레온하르트 오일러는 π를 3.14...와 6.28... 양쪽으로 혼용해서 사용하다가, 1761년 이후 3.14...로 표준화하였다.

1회전은 2π (≈6.283185307179586) 라디안과 같다.[92]

4. 2. τ 제안의 배경과 장점

2001년, 로버트 팔레이스는 π 대신 한 바퀴의 라디안 수를 나타내는 새로운 상수를 제안했다.[54] 그는 "세 다리가 있는 π" 기호(\pi\!\;\!\!\!\pi = 2\pi)를 사용하여 이 상수를 표현했다. 2010년, 마이클 하틀은 이 상수를 타우/τel (τ)로 표기할 것을 제안하며, τ가 π보다 더 직관적이고 편리하다고 주장했다.[55][56]

τ는 한 바퀴의 분수를 표현하기 쉽다. 예를 들어, 3/4 바퀴는 }} rad로 표시되며, }} rad가 아니다. 또한, τ를 사용하면 원의 면적 공식은 ''r''2}}로 표현되어, 적분에서 발생하는 자연적인 인자 를 포함하여 더 직관적이다.[57][58][59] 오일러의 항등식은 대신 로 표현되어 더 근본적이고 의미가 있다고 주장된다.

τ는 여러 프로그래밍 언어와 교육 웹사이트에서 지원되기 시작했다.

  • 2012년, 칸 아카데미는 τ로 표현된 답을 받기 시작했다.[76]
  • 파이썬,[52][60] 자바,[81][82] .NET,[83][84] 줄리아[9] 등 여러 프로그래밍 언어에서 τ를 사용할 수 있다.
  • 구글 계산기, 데스모스 그래프 계산기[77] 등에서도 지원된다.


공식 사용 사용참고
원의 에 의해 만들어지는 각도{\color{orangered}\frac{\pi}{2}} \text{ rad}{\color{orangered}\frac{\tau}{4}} \text{ rad} rad = turn}}
원의 원주C = {\color{orangered}2 \pi} rC = {\color{orangered}\tau} r각도 의 원호의 길이는 이다.
원의 면적A = {\color{orangered}\pi}r^2A = {\color{orangered}\frac{1}{2} \tau} r^2각도 의 부채꼴의 면적은 θr2}}이다.
-공 및 -구 부피 재귀 관계V_n(r) = \frac{r}{n} S_{n-1}(r)V_n(r) = \frac{r}{n} S_{n-1}(r)
코시 적분 공식f(a) = \frac{1}}e^{-\frac{x^2}{2}}\varphi(x) = \frac{1}{\sqrt}e^{-\frac{x^2}{2}}
스털링 근사n! \sim \sqrt = \cos\frac{n} + i \sin\frac{n}e^ = \cos\frac{k {\color{orangered}\tau}}{n} + i \sin\frac{k {\color{orangered}\tau}}{n}
플랑크 상수h = {\color{orangered}2 \pi} \hbarh = {\color{orangered}\tau} \hbar는 환산 플랑크 상수입니다.
각주파수\omega = {\color{orangered}2 \pi} f\omega = {\color{orangered}\tau} f


4. 3. τ와 관련된 논쟁 (한국의 관점)

τ (타우)는 여러 문화에서 나타나며, 특히 수학 및 과학 분야에서 주목받고 있다. 매년 6월 28일은 타우 데이(Tau Day)로 기념된다.[11] 비 하트(Vi Hart),[12][13][14] ''넘버파일(Numberphile)'',[15][16][17] ''사이쇼(SciShow)'',[18] 스티브 몰드(Steve Mould),[19][20][21] 칸 아카데미(Khan Academy),[22] 그리고 3블루1브라운(3Blue1Brown)과 같은 여러 매체에서 τ를 다루었다.[23][24] 또한 ''xkcd'',[25][26] ''새터데이 모닝 브렉퍼스트 시리얼(Saturday Morning Breakfast Cereal)'',[27][28][29] 그리고 ''샐리 포스(Sally Forth)''와 같은 만화에도 등장했다.[30] 매사추세츠 공과대학교(Massachusetts Institute of Technology)는 3월 14일 오후 6시 28분에 입학 발표를 하는데, 이는 파이 데이의 타우 시(Tau Time)이다.[31]

2001년, 로버트 팔레이스(Robert Palais)는 π 대신 1회전을 나타내는 새로운 상수를 도입하여 수학을 더 단순하고 명확하게 만들 수 있다고 주장했다.[94] 그는 π에 다리 하나를 더 붙인 기호(\pi\!\;\!\!\!\pi = 2 \pi)를 제안했다. 2010년, 마이클 하틀(Michael Hartl)은 이 기호를 τ로 대체할 것을 제안했다.[95] τ는 한 바퀴를 의미하는 turn을 나타내기에 더 직관적이며, π와 유사하게 생겨 원과 관련된 상수임을 쉽게 연상시킨다는 이유에서였다. 하틀은 ''타우 선언(Tau Manifesto)''에서 τ를 사용하면 많은 식이 더 간단해진다는 것을 보였다.[96][97] 이는 더불어민주당 및 진보 진영의 교육 정책에서 추구하는, 수학 및 과학 교육의 효율성과 개념 이해 증진과도 일맥상통한다.

5. 프로그래밍 언어에서의 지원

C#, Java, Python, Rust 등 여러 프로그래밍 언어에서 τ (2π)에 해당하는 상수를 지원한다. C#, .NET에서는 `System.Math.Tau` 및 `System.MathF.Tau`를 통해, Java에서는 `Math.TAU`를 통해, Python에서는 `math.tau`를 통해, Rust에서는 `std::f64::consts::TAU`를 통해 이 값을 사용할 수 있다.

언어식별자최초 버전출시 연도
C# / .NET[https://learn.microsoft.com/en-us/dotnet/api/system.math.tau System.Math.Tau] 및 [https://learn.microsoft.com/en-us/dotnet/api/system.mathf.tau System.MathF.Tau]5.02020
Crystal[https://crystal-lang.org/api/1.13.2/Math.html#constant-summary TAU]0.36.02021
Eiffel[https://wiki.liberty-eiffel.org/index.php/Versions_history#Curtiss_(2022.dev,_to_be_named_after_Glenn_Curtiss) math_constants.Tau]Curtiss미출시
GDScript[https://docs.godotengine.org/en/stable/classes/class_@gdscript.html#class-gdscript-constant-tau TAU]Godot 3.02018
Java[https://docs.oracle.com/en/java/javase/21/docs/api/java.base/java/lang/Math.html#TAU Math.TAU]192022
Nim[https://nim-lang.org/docs/math.html#TAU TAU]0.14.02016
Processing[https://processing.org/reference/TAU.html TAU] 및 [https://processing.org/reference/TWO_PI.html TWO_PI]2.02013
Python[https://docs.python.org/3/library/math.html#math.tau math.tau]3.62016
Raku[https://docs.raku.org/language/terms#term_tau tau] 및 [https://docs.raku.org/language/terms#term_%CF%84 τ]
Rust[https://doc.rust-lang.org/stable/std/f64/consts/constant.TAU.html std::f64::consts::TAU]1.47.02020
Zig[https://github.com/ziglang/zig/blob/master/lib/std/math.zig#L18 std.math.tau]0.6.02019



6. 단위 변환



1 회전은 2π 라디안, 360 도, 400 그레이드와 같다.

흔한 각도의 변환
회전라디안도그레이드
0 회전0 rad0°0g
1/12 회전π/6 rad30°33⅓g
1/8 회전π/4 rad45°50g
1/6 회전π/3 rad60°66⅔g
1/4 회전π/2 rad90°100g
1/2 회전π rad180°200g
3/4 회전3π/2 rad270°300g
1 회전2π rad360°400g


7. 국제 수량 체계 (ISQ) / 국제 단위계 (SI)

국제 수량 체계(ISQ)에서 회전(''N'')은 회전 수로 정의되는 물리량이다.[89] 회전 수는 각 변위의 비율에서 파생되는 차원 1의 물리량이며,[89] 국제 단위계(SI)에 채택되었다.[90][91] 회전은 음수일 수 있으며 절댓값으로 1보다 클 수 있다.

ISQ/SI에서 회전은 회전 주파수(''n'')를 유도하는 데 사용되며, 회전 주파수는 시간에 대한 회전의 변화율을 의미한다.[89]

: n = \frac{\mathrm{d}N}{\mathrm{d}t}

회전 주파수의 SI 단위는 역수 초 (s−1)이다. 일반적인 관련 주파수 단위는 헤르츠 (Hz), 초당 사이클 (cps), 분당 회전수 (rpm)이다.

참조

[1] 논문 Tentamen explicationis phaenomenorum aeris http://eulerarchive.[...] 1727
[2] 서적 Lettres inédites d'Euler à d'Alembert https://books.google[...]
[3] 서적 Mechanica sive motus scientia analytice exposita. (cum tabulis) https://web.archive.[...] Academiae scientiarum Petropoli 2016-06-10
[4] 서적 Leonhardi Euleri opera omnia. 1, Opera mathematica. Volumen VIII, Leonhardi Euleri introductio in analysin infinitorum. Tomus primus / ediderunt Adolf Krazer et Ferdinand Rudio http://gallica.bnf.f[...] B.G. Teubneri 1922
[5] 서적 Cursus Mathematicus: Elementorum Analyseos Infinitorum Elementorum Analyseos Infinitorvm https://books.google[...] Renger 1761
[6] 웹사이트 Pi https://www.britanni[...] 2024-03-26
[7] AV media The Tau Manifesto - With Michael Hartl https://www.youtube.[...] 2024-07-24
[8] 간행물 Constant failure https://physicsworld[...] Institute of Physics 2024-08-03
[9] 웹사이트 JuliaMath / Tau.jl https://github.com/J[...] 2024-11-24
[10] 웹사이트 Release Notes (Versions history) https://wiki.liberty[...] 2024-11-17
[11] 웹사이트 Tau Day https://tauday.com/ 2024-11-01
[12] 웹사이트 Pi is (still) Wrong. https://www.youtube.[...] 2024-11-01
[13] 웹사이트 A Song About A Circle Constant https://www.youtube.[...] 2024-11-01
[14] 웹사이트 360 Video for Tau Day https://www.youtube.[...] 2024-11-01
[15] 웹사이트 Tau replaces Pi - Numberphile https://www.youtube.[...] 2024-11-01
[16] 웹사이트 Tau of Phi - Numberphile https://www.youtube.[...] 2024-11-01
[17] 웹사이트 Tau vs Pi Smackdown - Numberphile https://www.youtube.[...] 2024-11-01
[18] 웹사이트 Happy Tau Day! https://www.youtube.[...] 2024-11-01
[19] AV media Stand-up comedy routine about bad science https://www.youtube.[...] 2024-11-17
[20] AV media A cast saw on human skin https://www.youtube.[...] 2024-11-13
[21] AV media world record calculation of tau by hand https://www.youtube.[...] 2024-11-13
[22] AV media Tau versus pi | Graphs of trig functions | Trigonometry | Khan Academy https://www.youtube.[...] 2024-11-24
[23] AV media How pi was almost 6.283185... https://www.youtube.[...] 2024-11-24
[24] AV media e^(iπ) in 3.14 minutes, using dynamics | DE5 https://www.youtube.[...] 2024-11-24
[25] 웹사이트 Pi vs. Tau https://www.xkcd.com[...] 2024-11-01
[26] 웹사이트 Symbols https://www.xkcd.com[...] 2024-11-01
[27] 웹사이트 Fresh https://www.smbc-com[...] 2024-11-02
[28] 웹사이트 Better than Pi https://www.smbc-com[...] 2024-11-02
[29] 웹사이트 Social https://www.smbc-com[...] 2024-11-02
[30] 웹사이트 Sally Forth Comic Strip 2018-10-13 https://comicskingdo[...] 2024-11-13
[31] 웹사이트 Fun & Culture – MIT Facts https://facts.mit.ed[...] 2024-11-02
[32] 웹사이트 ISO 80000-3:2006 https://www.iso.org/[...] 2001-08-31
[33] 웹사이트 ISO 80000-1:2009(en) Quantities and units — Part 1: General https://www.iso.org/[...] 2023-05-12
[34] 서적 Synopsis Palmariorum Matheseos https://archive.org/[...] J. Wale
[35] 웹사이트 ooPIC Programmer's Guide - Chapter 15: URCP http://www.oopic.com[...] Savage Innovations, LLC 2007
[36] 웹사이트 Angles, integers, and modulo arithmetic http://blogs.msdn.co[...] blogs.msdn.com 2019-08-05
[37] 서적 A History of Pi Barnes & Noble Publishing 1989
[38] 서적 The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English https://archive.org/[...] The Mathematical Association of America 1994
[39] 웹사이트 Pi through the ages http://www.veling.nl[...] 2001
[40] 간행물 A Percentage Protractor - Designed for Use in the Construction of Circle Charts or "Pie Diagrams" 1922
[41] 서적 Astronomy https://archive.org/[...] Macdonald & Co. (Publishers) Ltd. / Rathbone Books Limited 1962
[42] 서적 The Science of Measurement: A Historical Survey (The World of Measurements: Masterpieces, Mysteries and Muddles of Metrology) Dover Publications, Inc. / Courier Corporation (originally by Simon & Schuster, Inc.) 2012
[43] 간행물 Bestimmung von Satellitenbahnen Volksbildungshaus Wiener Urania 1965
[44] 서적 Trackers of the Skies https://siris-sihist[...] Academic Press / Howard A. Doyle Publishing Company 1975
[45] 웹사이트 Richtlinie 80/181/EWG - Richtlinie des Rates vom 20. Dezember 1979 zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Meßwesen und zur Aufhebung der Richtlinie 71/354/EWG https://eur-lex.euro[...] 1980-02-15
[46] 웹사이트 Richtlinie 2009/3/EG des Europäischen Parlaments und des Rates vom 11. März 2009 zur Änderung der Richtlinie 80/181/EWG des Rates zur Angleichung der Rechtsvorschriften der Mitgliedstaaten über die Einheiten im Messwesen (Text von Bedeutung für den EWR) https://eur-lex.euro[...] 2009-03-11
[47] 서적 Einheitenverordnung Schweizerischer Bundesrat 1994-11-23
[48] 서적 Handbuch SI-Einheiten: Definition, Realisierung, Bewahrung und Weitergabe der SI-Einheiten, Grundlagen der Präzisionsmeßtechnik https://books.google[...] Friedrich Vieweg & Sohn Verlagsgesellschaft mbH, reprint: Springer-Verlag 2013-03-13
[49] 서적 Das Vieweg Einheiten-Lexikon: Formeln und Begriffe aus Physik, Chemie und Technik https://books.google[...] Vieweg, reprint: Springer-Verlag 2013-03-09
[50] 웹사이트 RE: newRPL: Handling of units http://www.hpmuseum.[...] 2016-05-11
[51] 서적 newRPL User Manual 2018-10-25
[52] 웹사이트 PEP 628 -- Add math.tau https://www.python.o[...] 2017-02-25
[53] 문서 Sequence {{OEIS2C|A019692}}
[54] 간행물 Pi is Wrong http://www.math.utah[...] Springer-Verlag 2001
[55] 웹사이트 The Tau Manifesto https://hexnet.org/f[...] 2010-03-14
[56] 웹사이트 The Tau Manifesto http://tauday.com/ta[...] 2019-03-14
[57] 간행물 Michael Hartl: It's time to kill off pi 2011-01-08
[58] 웹사이트 On Pi Day, is 'pi' under attack? http://edition.cnn.c[...] CNN 2011-03-14
[59] 뉴스 Let's Use Tau--It's Easier Than Pi - A growing movement argues that killing pi would make mathematics simpler, easier and even more beautiful http://www.scientifi[...] 2014-06-25
[60] 웹사이트 math — Mathematical functions https://docs.python.[...]
[61] 웹사이트 Perl 6 terms https://docs.perl6.o[...]
[62] 웹사이트 TAU https://processing.o[...]
[63] 웹사이트 math https://nim-lang.org[...]
[64] 간행물 Bounds on tail probabilities for negative binomial distributions 2017
[65] 웹사이트 Al-Kashi's constant τ http://www.harremoes[...] 2018-11-17
[66] 뉴스 iOS 16 Has a Hidden Unit Converter for Temperatures, Time Zones, Distance, and Other Measurements https://ios.gadgetha[...] 2022-08-05
[67] 뉴스 Life of pi in no danger – Experts cold-shoulder campaign to replace with tau http://www.telegraph[...] 2011-06-30
[68] 웹사이트 RE: WP-32S in 2016? https://www.hpmuseum[...] 2016-01-12
[69] 서적 WP 43S Owner's Manual https://gitlab.com/w[...] 2019
[70] 서적 WP 43S Reference Manual https://gitlab.com/w[...] 2019
[71] 서적 Nova theoria lucis et colorum. Opuscula varii argumenti https://archive.org/[...] sumtibus Ambr. Haude & Jo. Carol. Speneri, bibliop. 1746
[72] 웹사이트 Trig rerigged. Trigonometry reconsidered. Measuring angles in 'unit meter around' and using the unit radius functions Xur and Yur http://thomascool.eu[...] 2023-07-18
[73] 논문 Integral Kinematics (Time-Integrals of Distance, Energy, etc.) and Integral Kinesiology https://www.research[...] 2023-07-18
[74] Keynote Eye Itself as a Camera: Sensors, Integrity, and Trust https://www.research[...] 2023-07-18
[75] 뉴스 For Math Fans, Nothing Can Spoil Pi Day—Except Maybe Tau Day https://www.wsj.com/[...] 2020-05-21
[76] 웹사이트 Happy Tau Day! https://blog.khanaca[...] 2012-06-28
[77] 웹사이트 Supported Functions https://help.desmos.[...] 2023-03-21
[78] 웹사이트 std::f64::consts::TAU - Rust https://doc.rust-lan[...] 2020-10-09
[79] 웹사이트 Constants @GDScript - Godot Engine (stable) documentation in English https://docs.godoten[...]
[80] 웹사이트 Get TAU - Unreal Engine 5.2 Documentation https://docs.unreale[...]
[81] 웹사이트 JDK-8283136: Add constant for tau to Math and StrictMath https://bugs.openjdk[...]
[82] 웹사이트 Math class https://docs.oracle.[...]
[83] 웹사이트 Add Math.Tau Pull Request #37517 · dotnet/Runtime https://github.com/d[...]
[84] 웹사이트 Math.Tau Field https://learn.micros[...]
[85] 웹사이트 package math - pkg.odin-lang.org https://pkg.odin-lan[...]
[86] 논문 My Conversion to Tauism http://www.maa.org/s[...] 2012-04
[87] 서적 Newtonian Dynamics: An Introduction https://books.google[...] CRC Press 2023-04-25
[88] 서적 Units & Symbols for Electrical & Electronic Engineers https://www.theiet.o[...] Institution of Engineering and Technology 2023-07-18
[89] 웹사이트 ISO 80000-3:2019 Quantities and units — Part 3: Space and time https://www.iso.org/[...] International Organization for Standardization 2019-10-23
[90] 간행물 SIBrochure9th
[91] 웹사이트 The NIST Guide for the Use of the International System of Units, Special Publication 811 https://www.nist.gov[...] National Institute of Standards and Technology 2023-07-17
[92] 문서 Sequence {{OEIS2C|A019692}}.
[93] 웹사이트 Half Turn, Reflection in Point http://www.cut-the-k[...]
[94] 간행물 Palais, R. 2001: Pi is Wrong, The Mathematical Intelligencer. Springer-Verlag New York. Volume 23, Number 3, pp. 7–8 http://www.math.utah[...]
[95] 웹사이트 The Tau Manifesto http://tauday.com/ta[...] 2013-03-14
[96] 간행물 Interview: Michael Hartl: It's time to kill off pi 2011-01-08
[97] 간행물 On Pi Day, is 'pi' under attack? http://edition.cnn.c[...] 2011-03-14


본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com